Perspectiva axonométrica

La perspectiva axonométrica es un sistema de representación gráfica consistente en representar elementos geométricos o volúmenes en un plano mediante proyección ortogonal u oblicua referida a tres ejes ortogonales, de tal forma que conserven sus proporciones en cada una de las tres direcciones del espacio: altura, anchura y longitud.

La perspectiva axonométrica cumple dos propiedades importantes que la distinguen de la perspectiva cónica:

• La escala del objeto representado no depende de su distancia al observador.
• Dos líneas paralelas en la realidad son también paralelas en su representación axonométrica.

Axonometría ortogonal

Este sistema se subdivide en dos principales, el sistema axonométricoortogonal y el sistema axonométrico oblicuo.

La diferencia entre ambos es la dirección de los rayos de proyección respecto del plano en el que se proyectan (proyección ortogonal o proyección oblicua).

Axonometría oblícua

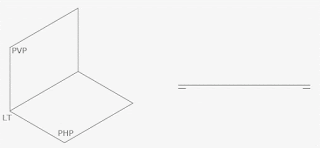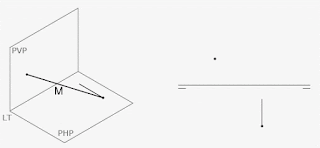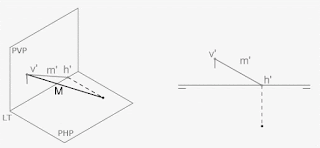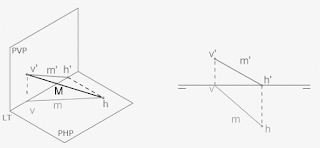
Los planos que intervienen en este sistema son cuatro: tres planos perpendiculares entre sí que forman un triedro trirrectángulo y un plano de proyección principal (desde ahora plano del cuadro) en el que se apoya el triedro anterior, en un vértice o una de sus caras.

Las proyecciones de las aristas del triedro sobre el plano del cuadro son los ejes de la axonometría.

 Cuando proyectamos sobre el plano del cuadro un eje axonométrico su dimensión queda reducida (coeficiente de reducción CR) originándose una relación de proporcionalidad entre esta y la real.

• En la axonometría ortogonal la reducción afecta a los tres ejes.
• En la axonometría oblicua la reducción solamente afecta a un eje

Sistema axonométrico ortogonal:

Se divide en tres subsistemas:

• Isométrico: El más utilizado por su comodidad. Los tres ejes forman el mismo ángulo entre sí.
• Dimétrico: Dos de los ángulos entre ejes son iguales.
• Trimétrico: Los tres ángulos son distintos.

 Sistema axonométrico oblicuo:

Tiene muchas variantes, algunas de las más conocidas son:

• Perspectiva caballera: Muy cómoda para trabajar en verdadera magnitud con una de las caras.
• Perspectiva militar: Aquella en la que la planta es la que esta en verdadera magnitud. Es muy usada en las perspectivas de arquitectura e ingeniería civil.

Perspectiva caballera

Perspectiva militar

Read More

Planos

Planos:

    Un plano es una superficie plana ilimitada, sin espesor.

El plano es uno de los elementos geométricos básicos.

Tiene dos dimensiones planas (X e Y) y se puede definir de varias formas :

• Tres puntos no alineados definen un plano.
• Un punto y una recta exterior al punto definen un plano.
• Dos rectas paralelas o dos rectas que se cortan también definen un plano.

Un plano no tiene proyección (la proyección de los infinitos puntos que lo componen daría como resultado una mancha de puntos), por este motivo los planos se representan en el sistema diédrico por sus trazas.

Todo plano en el espacio del sistema diédrico genera automáticamente dos trazas en forma de dos rectas contenidas en los dos planos proyectantes. Una traza vertical, en el plano de proyección vertical, y otra traza horizontal, en el plano de proyección horizontal.

Si tenemos las trazas de dos rectas que se cortan o que son paralelas, podemos conseguir las trazas del plano definido por dichas rectas uniendo sus trazas homónimas, esto es, por un lado las trazas verticales y por otro lado las trazas horizontales de las dos rectas.

Un plano en el espacio se marca con una letra griega mayúscula (α, β,…).

A la traza vertical de un plano se le denomina con la letra minúscula v y el subíndice α (u otra letra griega que define el plano) y a la traza horizontal de un plano se le denomina con la letra minúscula h y el mismo subíndice α (o la letra griega que le corresponda).

Sistemas para definir planos:

•  Plano definido por dos rectas que se cortan:

       Ya hemos comentado que dos rectas que se cortan definen un plano.          También sabemos que dos rectas que se cortan tienen un punto común.

           En la figura siguiente     se puede ver cómo se dibuja un plano definido por            dos rectas que se cortan, dibujando las trazas del plano por las trazas              homónimas de las rectas dadas.

           

• Plano definido por dos rectas paralelas

        Ya hemos comentado que dos rectas paralelas definen un plano. También     sabemos que dos rectas paralelas tienen sus proyecciones paralelas.

En la figura siguiente se puede ver cómo se dibuja un plano definido por dos rectas paralelas, dibujando las trazas del plano por las trazas homónimas de las rectas dadas.

• Plano definido por una recta y un punto

      Una recta y un punto exterior a ella definen un plano. Para dibujar el plano que forman una recta y un punto debemos coger un punto cualquiera de la recta y trazar la recta que definen el punto dado y el punto que hemos elegido en la recta, lo que da lugar a dibujar un plano definido por dos rectas que se cortan, que ya sabemos cómo se hace.

En la figura siguiente se puede ver cómo se dibuja un plano definido por una recta y un punto exterior a ella.

Intersección entre planos (método general):

Para hallar la intersección de dos planos dados hallamos los puntos de corte de sus trazas que nos determinará la recta de intersección que pasa por esos dos puntos.

Read More

Rectas

Rectas:

Toda recta en el espacio del sistema diédrico genera automáticamente dos proyecciones en forma de dos rectas. Una proyección vertical, en el plano de proyección vertical, y otra proyección horizontal, en el plano de proyección horizontal.
Si tenemos las proyecciones de dos puntos cualesquiera, podemos conseguir las proyecciones de la recta definida por dichos puntos uniendo sus proyecciones homónimas, esto es, por un lado las proyecciones verticales y por otro lado las proyecciones horizontales de los dos puntos.

 Trazas:

Son los puntos de intersección de una recta con los planos de proyección, así pues, una recta puede tener dos trazas como máximo: una vertical que denominaremos Vr, y otra horizontal que llamaremos Hr.

 

 Tipos de rectas:

•  Rectas paralelas a uno de los planos de proyección:

 

• Recta perpendicular a un plano de proyección:

 

 

 

• Recta oblicua a los planos de proyección:

Read More

El punto

           El punto

   En el caso de trabajar con tres planos de proyecciones, a la distancia que hay desde el punto al Plano de Perfil se la denomina Desviación. La proyección vertical de un punto se marca con la letra mayúscula correspondiente y el subíndice 2. La proyección horizontal de un punto se marca con la letra mayúscula correspondiente y el subíndice 1. En caso de trabajar con el plano de perfil, la proyección de perfil de un punto se marca con la letra mayúscula correspondiente rodeada de paréntesis ( ).

      Representación por coordenadas: 

Podemos definir cualquier punto dando tres coordenadas en la forma: (X, Y, Z), que se corresponden con X=desviación, Y=alejamiento y Z=cota, pudiendo tener valores positivos o negativos.

Posiciones generales del punto: 

Un punto en el espacio puede tener cualquier situación, pero según sea su posición relativa a los planos de proyección, presentan características de representación especiales

•  Los puntos situados en el primer Cuadrante siempre tienen la proyección vertical encima de la LT y la proyección horizontal debajo de la LT. 
•  Los puntos situados en el segundo Cuadrante siempre tienen la proyección vertical y la proyección horizontal encima de la LT. 
• Los puntos situados en el tercer Cuadrante siempre tienen la proyección vertical debajo de la LT y la proyección horizontal encima de la LT. 
• Los puntos situados en el cuarto Cuadrante siempre tienen la proyección vertical y la proyección horizontal debajo de la LT. 
• Los puntos situados en el plano Horizontal de proyección siempre tienen cota cero. 
• Los puntos situados en el plano Vertical de proyección siempre tienen alejamiento cero.
•  Los puntos situados en los planos bisectores siempre tienen iguales la cota y el alejamiento. 
• Los puntos situados en la Línea de Tierra siempre tienen cota y alejamiento cero. 

Existen 17 puntos notables en el Sistema Diédrico situados en los ocho octantes, en los cuatro bisectores, en los cuatro planos de proyección y en la LT. A la representación de estos 17 puntos se la conoce como alfabeto del punto.

Read More

Introducción al Sistema Diédrico

El Sistema Diédrico es un Sistema de Representación que se basa en una Proyección Paralela o Cilíndrica Ortogonal con dos Planos de Proyección, y en consecuencia, con dos proyecciones. En algunos casos se trabaja con tres planos de proyección, y por lo tanto con tres proyecciones. Por cada plano de proyección se obtienen una proyección. Los dos planos de proyección principales se cortan perpendicularmente en posiciones vertical y horizontal, dividiendo el espacio en cuatro zonas. A los planos de proyección se les denomina Plano Vertical de Proyección (PV o V) y Plano Horizontal de Proyección (PH o H). Aunque se representan con límites, en realidad son ilimitados, ya que son imaginarios. A la línea de intersección de los planos de proyección se la denomina Línea de Tierra (LT). A los cuatro espacios en los que queda divido el espacio general por los planos de proyección, se les denomina Diedros o Cuadrantes. El nombre Sistema Diédrico proviene de Diedro.

Cada vez que se posiciona un elemento en el espacio, automáticamente se obtienen sus dos proyecciones en los planos vertical y horizontal de proyección. A estas proyecciones se las denomina proyección vertical y proyección horizontal. Para convertir estos dos planos en uno solo, se abate uno de los planos sobre el otro, girando sobre la Línea de Tierra (LT), que hace las veces de bisagra, de forma que queden superpuestos. En el abatimiento se llevan consigo sus proyecciones. Después de realizado el abatimiento, junto con sus proyecciones, se obtiene un único plano de trabajo, con el único indicador de la Línea de Tierra (LT) como medio de referencia. La Línea de Tierra se marca con una línea fina horizontal y dos pequeñas rayitas debajo de sus extremos. La proyección vertical queda encima de la LT y la proyección horizontal queda debajo de  la LT. 

En ocasiones es interesante imaginar dos planos que dividen a los Cuadrantes en dos partes iguales. A estos planos se les conoce como Planos Bisectores. Los Planos de Proyección dividen el espacio en cuatro Cuadrantes. Los Planos Bisectores y los Planos de Proyección dividen el espacio en ocho Octantes 

Read More